モーターの進化と応用設計その2 〜応用設計編〜

こんにちは。樋詰です。

今回は、前回に引き続きモーターについてのお話です。
前回はモーターの進化についてお話ししましたが、今回はロボットへの適用を考察します。

このモーター、ここに使えるかな？

ある目的のためにモーターを選定していると「これ、使えるかな？」という場面ありますよね？
とりあえず使ってみて、上手く動けばOK、ダメだったら大きなモーターで再度トライする・・・というやり方でも、とりあえず前には進めます。
きっちり計算しようとしても電気回路の設計などと比べると趣が異なるし、モーターの教科書には実用的なことは書いてないし・・・などなど、ちょっと取っ掛かり難いですね。
でも、次のように案外簡単な実験で分かります。

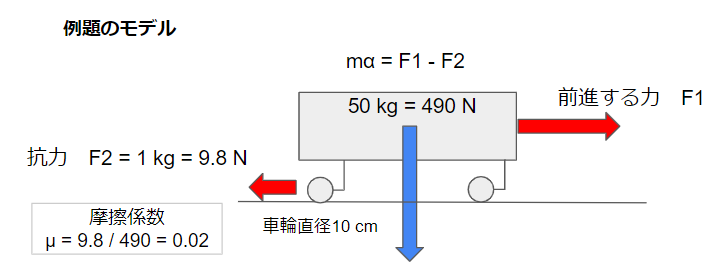
例題　このモーターでカート（台車）を動かせるか？

📌 カートの条件（これだけ分かれば、ほぼOK）

カート質量　50 kg

モーター　　定格トルク1Nm、4個

ホイール　　直径10cm

摩擦係数　　抗力を実測して求める

運動の第2法則

例題モデルの運動方程式を考えると：

$F_1-F_2=mα$

$前進する力F_1 (N)、抗力F_2(N)、質量 m(kg)、加速度 α(m/s^2)$

となります。
ここで、抗力は転がり抵抗や摩擦によるもので、前進する力に対して逆向きに働きます。
方程式の左辺がマイナスでは前進出来ませんから、このカートを前進させる条件は：

$F_1>F_2$

抗力 $F_2$ を測る・・・ $F_1$ との大小関係は大丈夫？

プッシュプルゲージやバネばかりを使って $F_2$ を測ります。
無限に緩慢に押す（引く）ことでカートが動き出したときの値です。学校で実験しましたね。
実測の結果は、1 kg = 9.8 N でした。
4つのモーターを合計した力 $F_1$ が 9.8 Nを超えていれば動かせます。
このモーターの定格トルクは 1 Nmでした。あれれ、足りない・・・では、ありませんね（笑）むしろ余裕であることが分かります。ここで車輪の直径を使います。
摩擦係数 $μ$ も求まります。